В статье рассмотрены простые конечные автоматы и их реализация на C++ с помощью switch-конструкций, таблиц времени исполнения и библиотеки Boost Statechart.
Введение
Грубо говоря, конечный автомат (Finite State Machine), глазами пользователя – это черный ящик, в который можно что-то передать и что-то оттуда получить. Это очень удобная абстракция, которая позволяет скрыть сложный алгоритм, кроме того конечные автоматы очень эффективны.
Конечные автоматы изображают в виде диаграмм состоящих из состояний и переходов. Поясню на простом примере:
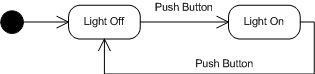
Как вы наверное догадались – это диаграмма состояний лампочки. Начальное состояние обозначается черным кружком, переходы стрелками, некоторые стрелки подписаны – это события после которых автомат переходит в другое состояние. Итак, сразу из начального состояния, мы попадаем в состояние Light Off – лампа не горит. Если нажать кнопку, то автомат изменит свое состояние и перейдет по стрелке помеченной Push Button, в состояние Light On – лампа горит. Перейти из этого состояния можно опять же по стрелке, после нажатия кнопки, в состояние Light Off.
Также широко используются таблицы переходов:
| Текущее состояние | Событие | Состояние после перехода | Действие |
| Light Off | Push Button | Light On | Загорается лампа |
| Light On | Push Button | Light Off | Лампа гаснет |
Практическое применение автоматов
Конечные автоматы широко используются в программировании. Например очень удобно представить работу устройства в виде автомата. Это сделает код проще и позволит легко с ним экспериментировать и поддерживать.
Также конечные автоматы применяют для написания всевозможных парсеров и анализаторов текста, с помощью них можно эффективно проводить поиск подстрок, регулярные выражения тоже транслируются в конечный автомат.
Для примера мы реализуем автомат для подсчета чисел и слов в тексте. Для начала договоримся, что числом будет считаться последовательность цифр от 0 до 9 произвольной длины, окруженная пробельными символами (пробел, табуляция, перевод строки). Словом будет считаться последовательность произвольной длины состоящая из букв и также окруженная пробельными символами.
Рассмотрим диаграмму:
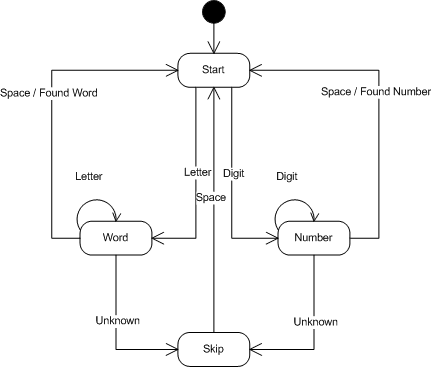
Из начального состояния мы попадаем в состояние Start. Проверяем текущий символ, и если он является буквой, то переходим в состояние Word по стрелке помеченной как Letter. Это состояние предполагает, что в данный момент мы рассматриваем слово, анализ дальнейших символов, либо подтвердит данное предположение, либо опровергнет. Итак, рассматриваем следующий символ, если он является буквой, то состояние не изменяется (обратите внимание на круговую стрелку помеченную как Letter). Если символ не является буквой, а соответствует пробельному символу, то это означает, что предположение было верным и мы обнаружили слово (делаем переход по стрелке Space в состояние Start). Если символ не является, ни буквой, ни пробелом, значит мы ошиблись в предположении и последовательность которую мы рассматриваем, не является словом (переходим по стрелке Unknown в состояние Skip).
В состоянии Skip мы находимся до тех пор, пока не будет встречен пробельный символ. После того как пробел был обнаружен мы переходим по стрелке Space в состояние Start. Это нужно, чтобы полностью пропустить строку не соответствующую нашему шаблону поиска.
После перехода в состояние Start, поиск цикл повторяется с начала. Ветвь с распознаванием чисел аналогична ветви распознавания слов.
Автомат с использованием switch-инструкций
Первое – возможные состояния:
enum States { State_Start, State_Number, State_Word, State_Skip }; |
Начальное состояние:
States state = State_Start; |
После чего мы итерируем по строке подсовывая автомату текущий символ. Сам автомат представляет собой инструкцию switch сначала выполняющей переход в секцию текущего состояния. Внутри секции есть конструкция if-else, которая в зависимости от события (пришедшего символа) изменяет текущее состояние:
const size_t length = text.length(); for (size_t i = 0; i != length; ++i) { const char current = text[i]; switch (state) { case State_Start: if (std::isdigit(current)) { state = State_Number; } else if (std::isalpha(current)) { state = State_Word; } break; case State_Number: if (std::isspace(current)) { |
Здесь смотрим на диаграмму – текущее состояние Number, событие Space (встречен пробельный символ), а значит найдено число:
FoundNumber(); state = State_Start; } else if (!std::isdigit(current)) { state = State_Skip; } break; case State_Word: if (std::isspace(current)) { FoundWord(); state = State_Start; } else if (!std::isalpha(current)) { state = State_Skip; } break; case State_Skip: if (std::isspace(current)) { state = State_Start; } break; } } |
Итог:
+ Высокая эффективность
+ Простота реализации для простых алгоритмов
— Тяжело поддерживать
Интерпретация времени выполнения
Идея данного подхода проста – надо создать таблицу переходов, заполнить ее, и потом, при наступлении события, найди в таблице следующее состояние и сделать переход:
enum Events { Event_Space, Event_Digit, Event_Letter, Event_Unknown }; void ProcessEvent(Events event); ... struct Transition { States BaseState_; Events Event_; States TargetState_; }; void AddTransition(States fromState, Events event, States toState); ... typedef std::vector<transition> TransitionTable; TransitionTable Transitions_; States CurrentState_; |
Заполнение таблицы:
AddTransition(State_Start, Event_Digit, State_Number); AddTransition(State_Start, Event_Letter, State_Word); AddTransition(State_Number, Event_Space, State_Start); AddTransition(State_Number, Event_Letter, State_Skip); AddTransition(State_Number, Event_Unknown, State_Skip); AddTransition(State_Word, Event_Space, State_Start); AddTransition(State_Word, Event_Digit, State_Skip); AddTransition(State_Word, Event_Unknown, State_Skip); AddTransition(State_Skip, Event_Space, State_Start); |
Получилось довольно наглядно. Платой за наглядность будет более медленная работа автомата, что впрочем, часто не имеет значения.
Чтобы автомат, при наступлении некоторых событий, мог оповестить некоторый код, можно добавить в структуру с информацией о переходе (Transition) указатель на функцию (Action), которая будет вызываться:
typedef void (DynamicMachine::*Action)(); struct Transition { States BaseState_; Events Event_; States TargetState_; Action Action_; }; ... void AddTransition(States fromState, Events event, States toState, Action action); ... AddTransition(State_Number, Event_Space, State_Start, &DynamicMachine::FoundNumber); |
Итог:
+ Гибкость и наглядность
+ Проще поддерживать
— Меньшая производительность по сравнению с switch-блоками
Интерпретация времени исполнения. Оптимизация по скорости
Можно ли объединить наглядность со скоростью? Сделать автомат настолько же эффективным, как автомат на switch-блоках вряд ли удастся, но сократить разрыв можно. Для этого надо из таблицы, построить матрицу, такую, чтобы для получения информации о переходе не выполнять поиск, а сделать выборку по номеру состояния и события:
struct Transition { States TargetState_; Action Action_; }; typedef std::vector<Transition> TransitionByEventsTable; typedef std::vector<TransitionByEventsTable> StatesTable; StatesTable States_; States CurrentState_; |
Здесь из вектора States_ по номеру текущего состояния, можно получить вектор с переходами (Transition), где индексом служит номер события. Таким образом поиск состояния для перехода выполняется за время O(1):
const TransitionByEventsTable& transitionByEvents = States_[CurrentState_]; const Transition& transition = transitionByEvents[event]; |
Достигается результат, за счет расхода памяти.
Итог:
+ Гибкость, наглядность
+ Эффективен
— Расход памяти (скорее всего несущественно)
Boost Statechart
Мы обсудили несколько способов самостоятельной реализации конечного автомата. Для разнообразия предлагаю рассмотреть библиотеку для построения автоматов из Boost. Данная библиотека очень мощная, предлагаемые возможности позволяют построить очень сложные конечные автоматы. Мы же рассмотрим ее довольно бегло.
Итак, сначала определим события:
namespace Events { struct Digit : boost::statechart::event<Digit> {}; struct Letter : boost::statechart::event<Letter> {}; struct Space : boost::statechart::event<Space> {}; struct Unknown : boost::statechart::event<Unknown> {}; } |
Саму машину (обратите внимание, что второй параметр шаблона – начальное состояние):
struct Machine : boost::statechart::state_machine<Machine, States::Start> {}; |
И собственно сами состояния. Внутри состояний требуется определить тип описывающий переходы (reactions), а если переходов несколько, то перечислить их в списке типов boost::mpl::list. Второй параметр шаблона simple_state – тип описывающий машину. Переходы описываются параметрами шаблона transition, парой Событие — Следующее состояние:
namespace States { struct Start : boost::statechart::simple_state<Start, Machine> { typedef boost::mpl::list < boost::statechart::transition<Events::Digit, States::Number>, boost::statechart::transition<Events::Letter, States::Word> > reactions; }; struct Number : boost::statechart::simple_state<Number, Machine> { typedef boost::mpl::list < boost::statechart::transition<Events::Space, States::Start>, boost::statechart::transition<Events::Letter, States::Skip>, boost::statechart::transition<Events::Unknown, States::Skip> > reactions; }; struct Word : boost::statechart::simple_state<Word, Machine> { typedef boost::mpl::list < boost::statechart::transition<Events::Space, States::Start>, boost::statechart::transition<Events::Digit, States::Skip>, boost::statechart::transition<Events::Unknown, States::Skip> > reactions; }; struct Skip : boost::statechart::simple_state<Skip, Machine> { typedef boost::statechart::transition<Events::Space, States::Start> reactions; }; } |
Машина построена, осталось только инициализировать ее и можно использовать:
Machine machine; machine.initiate(); ... machine.process_event(Events::Space()); |
Итог:
+ Гибкость, расширяемость
— Эффективность
Быстродействие
Я написал тестовую программу для проверки быстродействия построенных автоматов. Через автоматы я прогнал текст размером ~17 Мб. Вот результаты прогона:
Loading text Text length: 17605548 bytes 0.19 s Running BoostMachine Words: 998002, numbers: 6816 0.73 s Running DynamicMachine Words: 998002, numbers: 6816 0.56 s Running FastDynamicMachine Words: 998002, numbers: 6816 0.29 s Running SimpleMachine Words: 998002, numbers: 6816 0.20 s
Что осталось не рассмотренным
Неохваченными остались еще несколько реализаций конечных автоматов (рекомендую http://www.rsdn.ru/article/alg/Static_Finite_State_Machine.xml и http://www.rsdn.ru/article/alg/FiniteStateMachine.xml), генераторы строящие автоматы из описаний, библиотека Meta State Machine из Boost версии 1.44.0, а также формальные описания конечных автоматов. Со всем перечисленным любопытный читатель может ознакомиться самостоятельно.
Исходный код автоматов и тестовой программы
http://www.devexp.ru/wp-content/uploads/2011/02/state_machines.zip
Boost MSM по лично проведенным испытаниям скорости в 4 раза в среднем быстрее чем Boost State Chart, таким образом он сочетает в себе и скорость и гибкость, нет смысла писать свои велосипеды.
Одно но! MSM достаточно труден в освоении, но те, кто осилил State Chart, MSM так же осилит =)
Andrey
14 февраля 11 14:36
Подтверждаю: boost MSM в шесть раз быстрее!
niXman
5 сентября 11 19:41
Безусловно, Boost MSM быстр. Кроме того, таблица переходов в MSM выразительнее, чем указание списков transition индивидуально для каждого состояния Boost statechart (т.к. последнее принуждает программиста размежевать код, описывающий переходы и, тем самым, связанный по своему смыслу, что в свою очередь, добавляет в исходники синтаксический шум).
Но MSM очень прожорлив на этапе компиляции; моя попытка собрать машину с ~50 состояниями при помощи gcc4.5.2 на 32-битной платформе провалилась (привела к segfault). На этой же машине gcc4.7.0 заявил, что virtual memory exhausted. После долгих мучений справились лишь gcc4.3 и 4.6.4. Подозреваю, что если количество состояний ещё немного возрастёт — мне придётся использовать Statechart.
ko1ia
21 апреля 12 21:54
Просто и доступно, но с одним не согласен. Почему вы решили, что данную схему сложно поддерживать или вы утверждаете, что это только для простых алгоритмов? На мой взгляд вся сложно при парсинге протоколов и состоит в составлении корректного автомата, а уж поддерживать просто песня. Мы всегда знаем где мы руководствуясь лишь одной переменной СОСТОЯНИЕМ, минимизируя эффект побочных действий.
avk17
7 февраля 13 13:45
В Автоматах понятнее всего у
Шалыто Анатолий Абрамович
http://is.ifmo.ru/aboutus/shalyto/
http://is.ifmo.ru/automata/
Всё расписано.
Философ
18 декабря 14 14:54
На прошлых выходных Я Заработал в этом самом популярном казино
777азино ру
23 июля 18 1:27
1 год назад Я выиграл деньги
в этом онлайн-казино
вулкан platinum зеркало
27 июля 18 6:14
Не так давно Я Заработал в этом азартном заведении
азино777
17 августа 18 16:21
Absolutely with you it agree. It seems to me it is very good idea. Completely with you I will agree.
————
https://servers.expert/
JefferyNAWAY
8 сентября 23 8:23
7lx23j
Get free iPhone 15: https://xn--80aaanh1cwa2a.xn--p1ai/upload/go.php hs=161d725c03c159f841b212b1d9f7e389*
11 ноября 23 15:02
5oe6y2
* * * GET FREE iPhone 15: http://asoyinsaat.com/uploads/go.php * * * hs=161d725c03c159f841b212b1d9f7e389*
20 февраля 24 21:32